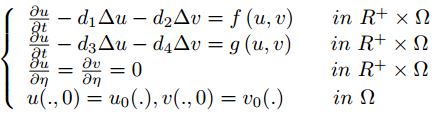Global solution of reaction diusion system with full matrix

  • Authors

    • Mebarki Maroua laboratoire de mathématique appliquée ,dunamique et modelisation univercité badji mokhta annaba
    • Moumeni Abdelkader laboratoire de mathématique appliquée
    2015-06-21
    https://doi.org/10.14419/gjma.v3i3.4683
  • Global Existence, Reaction Diffusion Systems, Lyapunov Functional.

  • Abstract

    The purpose of this paper is to prove the global existence in time of solutions for the strongly coupled reaction-diffusion system:



    with full matrix of diffusion coefficients. Our techniques of proof are based on Lyapunov functional methods and some \(L^{p}\) estimates. we show that global solutions exist. Our investigation applied for a wide class of the nonlinear terms f and g.

  • References

    1. [1] N. Alikakos, LP bounds of solutions of reaction-diffusion equations, Comm. Partial Differential Equations 4 (1979), 827--828.

      [2] H. Amann, Dynamic theory of quasilinear parabolic equations - I. Abstract evolution equations, Nonlinear Anal. 12 (1988), 895-919.

      [3] S. Bonaved, D. Schmitt, Triangular reaction-diffusion systems with integrable initial data, Nonlinear. Anal 33 (1998), 785--801.

      [4]K. Boukerrioua,existence of global solutions for a system of reaction-diffusion equations having a full matrix Ser. Math. Inform. Vol. 29, No 1 (2014), 91--103

      [5] T. Diagana, Some remarks on some strongly coupled reaction-diffusion equations, J.Reine. Angew., 2003.

      [6] R. Fisher, The advance of advantageous genes, Ann. Eugenics 7 (1937), 335--369.

      [7] H. Fujita, On the blowing up of solutions to the Cauchy problem for ∂u/∂t=Δu+u^{^{(σ+1)}} J. Fac. Sci. Univ. Tokyo Sect. A Math. 16 (1966), 105--113.

      [8] A. Haraux, M. Kirane, Estimation C1 pour des problèmes paraboliques semi-linéaires,Ann. Fac. Sci. Toulouse Math. 5 (1983), 265--280.

      [9] A. Haraux, A. Youkana, On a result of K. Masuda concerning reaction-diffusion equations, Tohoku. Math. J. 40 (1988), 159--163.

      [10] D. Henry, Geometric Theory of Semilinear Parabolic Equations, Lecture Notes in Math., 840, Springer Verlag, New York, 1981.

      [11] S. L. Hollis, R. H. Martin, M. Pierre, Global existence and boundedness in reaction diffusion systems, SIAM. J. Math. Anal. 18(3) (1987), 744--761.

      [12] J. I. Kanel and M. Kirane, Pointwise a priori bounds for a strongly coupled system of reaction-diffusion equations with a balance law, Math. Methods Appl. Sci. 21 (1998), 1227-1232.

      [13] I. Kanel, M. Kirane, Global existence and large time behavior of positive solutions to a reaction diffusion system, Differ. Integral Equ. Appl. 13(1--3) (2000), 255--264.

      [14] S. Kouachi, Global existence of solutions to reaction diffusion systems via a Lyapunov functional, Electron. J. Differential Equations (68) (2001), 1--10.

      [15] S. Kouachi, Global existence of solutions for reaction-diffusion systems with a full matrix of diffusion coe cients and nonhomogeneous boundary conditions,Electron. J. Qual. Theory Di er. Equ. 4 (2002), pp. 1-10.

      [16] S. Kouachi, Global existence of solutions in invariant regions for reaction-diffusion systems with a balance law and a full matrix of di usion coe cients,Electron. J. Qual. Theory Differ. Equ. 2 (2003), pp. 1-10.

      [17] S. Kouachi, Invariant regions and global existence of solutions for reaction-diffusion systems with full matrix of diffusion coefficients and nonhomogeneous boundary conditions, Georgian Math. J. 11 (2004), 349-359.

      [18] S. Kouachi, A. Youkana, Global existence and asymptotics for a class of reaction diffusion systems, Bull. Polish Acad. Sci. Math. 49(3), 2001.

      [19] R. H. Martin, M. Pierre, Nonlinear reaction-diffusion systems, in: Nonlinear Equations in the Applied Sciences, Math. Sci. Eng. Acad. Press, New York 1991.

      [20] K. Masuda, On the global existence and asymptotic behavior of solutions of reaction diffusion equations, Hokkaido Math. J. 12 (1983), 360--370.

      [21] A. Moumeni, L. Salah Derradji, Global existence of solution for reaction diffusion systems, IAENG, Int. J. Appl. Math. 40(2) (2010), 84--90.

      [22] A. Moumeni, L. Salah Derradji, Global existence of solution for reaction diffusion Systems with non diagonal matrix, Demonstratio Mathematica, Vol. XLV No 1( 2012 ).

      [23] J. D. Murray, Mathematical Biologie, 3rd ed., Interdisciplinary Applied Mathematics,Springer Verlag, 2002.

      [24] A. Pazy, Semigroups of linear operators and applications to partial differential equations,Applied Mathematical Siences, Springer--Verlag, New York, 1983.

      [25] M. Pierre, D. Schmitt, Blow up in reaction-diffusion systems with dissipation of mass,SIAM. J. Math. Anal. 42(1) (2000), 93--106.

      [26] B. Rebiai and S. Benachour, Global classical solutions for reactiondiffusion systems with nonlinearities of exponential growth, J. Evol. Equ.10 (2010), 511--527

      [27] F. Roth, Global solutions of reaction diffusion systems, Lecture Notes in Math. 1072,Springer Verlag, Berlin, 1984.

  • Downloads

    Additional Files

  • How to Cite

    Maroua, M., & Abdelkader, M. (2015). Global solution of reaction diusion system with full matrix. Global Journal of Mathematical Analysis, 3(3), 109-120. https://doi.org/10.14419/gjma.v3i3.4683

    Received date: 2015-04-25

    Accepted date: 2015-05-25

    Published date: 2015-06-21